Zasada działania silnika rakietowego cz. 3 – Siła ciągu rakiety

Ciąg jest siłą produkowaną przez system napędowy rakiety, który bezpośrednio oddziałuje na pojazd (w naszym przypadku rakietę). Jest to siła reakcji, której doświadcza nasza rakieta (jej struktura) poprzez wyrzut materii z dużą prędkością.

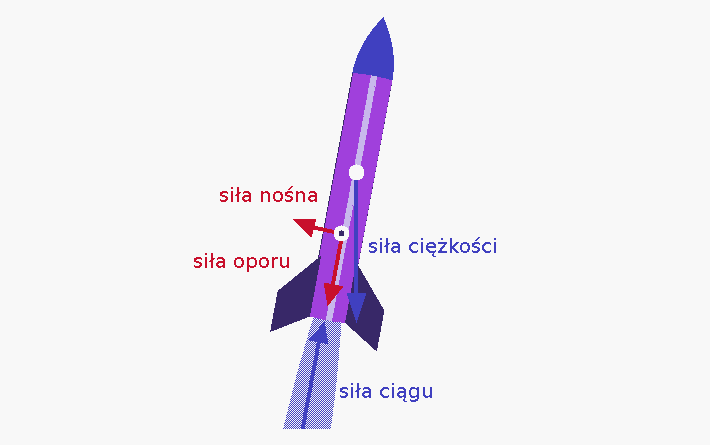
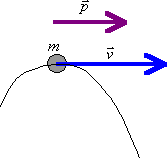
Wyrzut oczywiście musi nastąpić z odpowiednim ukierunkowaniem, aby jak najbardziej zoptymalizować kierunek, jak i prędkość poruszania się rakiety, aby poruszała się po torze, który jej nadamy, a nie w sposób randomowy (nieokreślony). Kolejnym ważnym założeniem jest pokonanie przez nasz napęd siły ciężkości i różnego rodzaju oporów działających na rakietę. Ten sam fenomen (siłę ciągu) możemy zaobserwować w naszych domach. Każdy, kto chodź raz podlewał rośliny wie, że do tej czynności należy użyć (zazwyczaj) węża ogrodowego. Siła, która powoduje odrzut węża do tyłu odpowiada również, w większej skali, za poruszanie się naszej rakiety. Zjawisko odrzutu podczas wystrzału z broni to ta sama historia. Wektor pędu skierowany w stronę linii ruchu naszego pocisku lub prochu strzelniczego równy jest odrzutowi pędu w tym samym kierunku, ale z przeciwnym zwrotem naszej lufy. Sam pęd w najprostszym ujęciu jest wielkością wektorową (tzn. posiada kierunek, zwrot, wartość i najczęściej też punkt przyłożenia) i zdefiniowany jest jako iloczyn masy i prędkości.

Wszystkie napędy statków (różnego rodzaju) generują swój ciąg, który powoduje ich ruch jako wydatek pędu wody, powietrza lubi innej substancji (chodzi tutaj przede wszystkim o udział jej masy), powodując przyspieszenie,  które skierowane jest w kierunku tylnej części statku ze zwrotem dodatnim według naszego układu odniesienia. Napędy rakiet różnią się znacząco od napędów innych statków. Różnica polega głównie na udziale masy ciał zewnętrznych na wytwarzanie ciągu samej rakiety. Cała masa, która ma służyć w założeniu za wytwarzanie ciągu, zawarta jest i zabrana w samej rakiecie. Definicyjne rakieta wytwarzać ma ciąg poprzez utratę własnej masy przy wystarczająco dużej prędkości gazów wylotowych. Ciąg przy uwzględnieniu zmiany pędu (w czasie) wyraża się wzorem:

gdzie:

dm/dt – zmiana masy w czasie,

v₂ – prędkość [m/s] (dlaczego v₂ – 2 zgodnie ze schematem przytoczonym w dalszej części artykułu),

ṁ – masowe natężenie przepływu lub strumień masy [kg/s].

Wzór przedstawiony powyżej reprezentuje całą siłę ciągu silnika przy ciśnieniu wylotowym z dyszy równym ciśnieniu otoczenia. Czyli wychodzi na to, że ograniczenia samego wzoru są całkiem duże. Trudno jest konstrukcyjne zaprojektować dyszę wylotową silnika tak, aby zawsze ciśnienie wylotowe było równe ciśnieniu otoczenia. Dochodzi natomiast do jeszcze większych komplikacji wtedy, gdy nasza rakieta przewidziana jest do lotów zarówno w próżni, jak i w atmosferze ziemskiej. Sama zmiana ciśnienia między ciśnieniem standardowym 1013,25 hPa (lub tak jak przyjmę w naszym założeniu 1,013 bara), a ciśnieniem w próżni (załóżmy, że mowa tutaj o próżni całkowitej) równym 10-7 mbara (dla uproszczenia przyjmę 0 barów), jest mniejsza niż między oponami (2,2 bara), które przecież widzimy na co dzień (nie ulegają one często eksplozji spowodowanej różnicą ciśnień), a ciśnieniem standardowym, ale jednak jest. Swoją drogą zastanawialiście się kiedyś, jak mierzy się „próżnię”? Przytoczę dwa sposoby. Po pierwsze mamy próżniomierz typu Pirani.

Próżniomierz ten wykorzystuje zjawisko przewodnictwa cieplnego gazu w zakresie od 0,0001 Pa do około 100 000 Pa. Wartość rezystancji drutu zależy od jego temperatury. Grzejemy nasz drut, a otaczający gaz go chłodzi. Następnie mierzymy prąd za pomocą prawa Ohma, mając już prąd, jesteśmy w stanie wyznaczyć wartość ciśnienia. Zwykle stosujemy to urządzenie do zgrubnego pomiaru, gdy nie zależy nam na bardzo dokładnych wręcz laboratoryjnych pomiarach. Drugi sposób to pomiar próżniomierzem jarzeniowym z zimną katodą (niepodgrzewaną zewnętrznie).

Składa się on z dwóch elektrod (anody i katody), do których przyłożone jest wysokie napięcie. Wskutek wysokiego pola elektrycznego elektrody (mające ładunek ujemny) zmierzają w kierunku anody, rozpoczynając swój ruch z katody. Po drodze zderzając się z cząsteczkami gazu, powodując ich jonizację i wyładowanie jarzeniowe. Pomiar ciśnienia odbywa się poprzez pomiar prądu jonowego, który jest proporcjonalny do ciśnienia gazu.

Wracając do wcześniejszej deliberacji. Ciśnienie otaczającego nas płynu wpływa, więc znacząco na siłę naszego ciągu.

Wielkość strzałek znajdujących się na schemacie wskazuje relatywną wartość siły ciśnienia działającej na części pokazane na rysunku naszej rakiety. Jak widzimy, względna wartość naszego ciśnienia wraz ze zbliżeniem się do miejsca opuszczenia przez gazy wylotowe naszego pojazdu zmniejsza się w sposób znaczący (mało pomijalny). Ciąg osiowy może zostać wyznaczony poprzez odpowiednie zsumowanie wszystkich ciśnień działających na rakietę, które mogą zostać określone na płaszczyźnie normalnej względem osi dyszy wylotowej. Tak jak pisałem wcześniej, nie rozwiązuje to jeszcze problemu dotyczącego dyszy wylotowej, ponieważ ma ona dalej stałą geometrię, jak również ciśnienie jest zmienne wraz z konfiguracją lotu lub też wysokością. Jest to problem, który niezwłocznie trzeba uwzględnić we wzorze. Przyjmuję za ciśnienie atmosferyczne symbol p3, za ciśnienie lokalne gazów opuszczających dyszę wylotową symbol p2, a za pole powierzchni otworu wylotowego symbol A2. Wszystko zgodnie ze schematem przedstawionym powyżej (żeby nie wprowadzać w błąd). Po uwzględnieniu nowo wprowadzonych symboli i zsumowaniu ich do poprzednio ustalonego wzoru możemy ustalić postać końcową:

Zwykło się dzielić ten wzór na dwa osobne człony z różnymi nazwami, pierwszy to „pęd ciągu”, a drugi to „ciśnienie ciągu”. Warto założyć, że w przypadku gdy ciśnienie wylotowe z silnika jest mniejsze co do wartości od ciśnienia płynów otaczających rakietę, „ciśnienie ciągu” przyjmuje wartości ujemne. Czy jest powód, dla którego można by podważyć poprawność powyższego wzoru? Nie do końca, dlatego, że do takiej sytuacji nigdy nie dojedzie. Zjawisko to jest mało efektywne i niepożądane. Rakiety z założenie projektuje się tak, aby ciśnienie gazów wylotowych było co najmniej równe lub minimalnie większe od ciśnienia płynów otaczających nasz statek kosmiczny. W przypadku gdy p₃ = 0, czyli gdy ciśnienie atmosferyczne równe jest 0, wzór upraszcza się do postaci:

Przy założeniu, że ciśnienie gazów wylotowych jest równe ciśnieniu zewnętrznemu (p₂ = p₃), mamy do czynienia z tzw. „optimum expansion ratio”.   Ponieważ ciśnienie otoczenia maleje wraz ze wzrostem wysokości, ciąg, jak i impuls właściwy będą rosły. Zmiana ta będzie wahała się w granicach od 10 do 30% całkowitego ciągu w typowym silniku rakietowym.

Źródło:

Rocket Propulsion Elements – GEORGE P. SUTTON, OSCAR BIBLARZ

Prawo Pascala, a próżnia dr Zbigniew Łukasiak